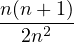
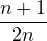
https://www.youtube.com/watch?v=JO29QpNQYqM

limn→∞( ) -1 -n sinn2 + ...+ sinn2 ≃ limn→∞( ) -1 n- n2 + ...+ n2
= limn→∞1+ ...+ n ---n2----
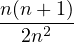= limn→∞n(n+ 1) --2n2---
= limn→∞n+ 1 -2n--
= 1 2.

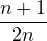With slightly more rigour:

limn→∞( 1 n) sin-2 + ...+ sin-2 n n ≃ limn→∞∑ k=1n{ k ( 1 )} -2 + k2O --4 n n
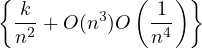= limn→∞∑ k=1n{ ( )} k-+ O (n3)O 1- n2 n4
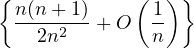= limn→∞{ ( )} n(n-+-1) 1- 2n2 + O n
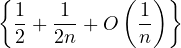= limn→∞{1 1 ( 1) } - + ---+ O -- 2 2n n
= 1 2.